Выборочное наблюдение

Добавлено в закладки: 0

Что такое выборочное наблюдение? Описание и определение понятия

Выборочное наблюдение – это статистическое наблюдение некоторой части выборки (совокупности), которая организуется так, чтобы обеспечивалось соответствие ее генеральной совокупности.

Выбранная часть элементов обязана отвечать двум требованиям: во-первых, она должна быть довольно многочисленной, чтобы имеющиеся закономерности могли бы проявиться в ней, во-вторых, процесс выборки обязан осуществляться объективно, вне зависимости от воли исследователя.

Именно при помощи выборочного наблюдения получают некоторые сведения при проведении переписи населения.

Статистическая совокупность

Статистическая совокупность — это множество единиц, которые обладают типичностью, массовостью, наличием вариации и качественной однородностью.

Статистическая совокупность состоит из существующих материально объектов (предприятия, работники, регионы, страны), является объектом статистического исследования.

Единица совокупности — это каждая конкретная единица статистической совокупности.

Одна и та же статистическая совокупность может быть однородной по одному признаку и неоднородной по другому.

Качественная однородность — это сходство всех единиц совокупности по какому-нибудь признаку и несходство по другим.

Отличия одной единицы совокупности от другой в статистической совокупности зачастую имеют количественную природу.

Числовые изменения значений признака различных единиц совокупности — это вариация.

Вариация признака — это числовое изменение признака (для числового признака) при переходе от одной к другой единицы совокупности.

Признак — это характерная черта, свойство или другая особенность явлений, единиц, объектов, которая может быть измерена или наблюдаема. Признаки делятся на качественные и количественные. Изменчивость и многообразие величины признака у отдельных единиц совокупности — это вариация.

Качественные (атрибутивные) признаки не поддаются количественному выражению (состав по полу населения). Числовые признаки имеют количественное выражение (состав по возрасту населения).

Показатель — это обобщающая качестванно-количественная характеристика какого-нибудь свойства единиц или совокупности в целом в конкретных условиях места и времени.

Система показателей — это совокупность показателей отражающих всесторонне изучаемое явление.

К примеру, изучают зарплату:

• Вариация признака — это ряд цифр
• Статистическая совокупность — это все сотрудники
• Признак — это оплата труда
• Качественная однородность — это начисленная заработная плата
• Единица совокупности — это каждый сотрудник

Выборка и генеральная совокупность

Основа статистического исследования — это множество данных, которые получены в итоге измерения одного или нескольких признаков. Наблюдаемая реально совокупность объектов, представленная статистически рядом наблюдений случайной величины — это выборка, а существующая гипотетически (домысливаемая) — это генеральная совокупность.

Генеральная совокупность может являться конечной (количество наблюдений N = const) или бесконечной (N = ∞), а выборка из генеральной совокупности — это результат всегда ограниченного ряда наблюдений. Количество наблюдений, которые образуют выборку — это объем выборки. Когда объем выборки довольно велик (n → ∞) выборка является большой, иначе это выборка ограниченного объема. Выборка является малой, когда при измерении случайной одномерной величины объем выборки не больше 30 (n <= 30), а при измерении нескольких одновременно (k) признаков в многомерном пространстве отношение n к k не больше 10 (n/k < 10). Выборка создает вариационный ряд, когда ее члены — это порядковые статистики, то есть выборочные значения случайной величины Х ранжированы (упорядочены по возрастанию), значения признака — это варианты.

Пример. Практически одна и та же отобранная случайно совокупность объектов — коммерческих банков административного округа Москвы, может рассматриваться как выборка из генеральной совокупности всех коммерческих банков данного округа, и как выборка из генеральной совокупности всех коммерческих банков Москвы и как выборка из коммерческих банков страны и так далее.

Главные методы организации выборки

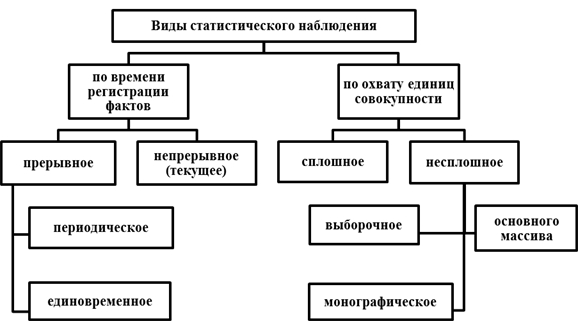
Содержательная интерпретация результатов и достоверность статистических выводов связана с репрезентативностью выборки, т.е. полнотой и адекватностью представления свойств генеральной совокупности, в отношении которой данную выборку считают представительной. Изучение статистических свойств совокупности возможно организовать двумя методами: при помощи несплошного и сплошного наблюдения. Сплошное наблюдение предусматривает обследование всех единиц исследуемой совокупности, а выборочное (несплошное) наблюдение — лишь его части.

Есть пять главных методов организации выборочного наблюдения:

1. Случайный простой отбор, при котором объекты случайно извлекаются из генеральной совокупности (к примеру, при помощи датчика случайных чисел или таблицы), при этом каждая из возможных выборок обладают равной вероятностью. Данные выборки называют собственно-случайными;

2. Простой отбор при помощи регулярной процедуры производится при помощи механической составляющей (к примеру, дня недели, даты, буквы алфавита, номера квартиры и так далее) и полученные таким методом выборки называют механическими;

3. Стратифицированный отбор заключён в том, что генеральная совокупность объема делится на слои или подсовокупности (страты) объема. Страты являют собой однородные объекты с точки зрения статистических характеристик (к примеру, население делят на страты по социальной принадлежности или возрастным группам; предприятия — по отраслям). Выборки в этом случае называют стратифицированными (или районированными, расслоенными, типическими);

4. Способы серийного отбора применяются для формирования гнездовых или серийных выборок. Они удобны, когда нужно обследовать сразу серию объектов или “блок” (к примеру, партию товара, продукцию некоторой серии или население при административно-территориальном делении страны). Отбор серий возможно произвести механическим или собственно-случайным методом. При этом производится сплошное обследование некоторой партии товара, или целой территориальной единицы (квартала или жилого дома);

5. ступенчатый (комбинированный) отбор может в себе сочетать сразу несколько методов отбора (к примеру, случайный и стратифицированный или механический и случайный); такая выборка является комбинированной.

Типы отбора

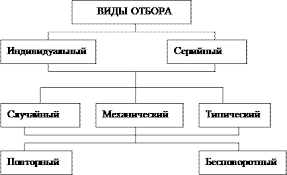
По виду различают групповой, индивидуальный, комбинированный отбор. В выборочную совокупность при индивидуальном отборе отбирают особые единицы генеральной совокупности, при групповом отборе — однородные качественно группы (серии) единиц, а комбинированный отбор предусматривает сочетание второго и первого типов.

По способу отбора различают бесповторную и повторную выборку.

Бесповторный — это отбор, при котором единица, которая попала в выборку в исходную совокупность не возвращается и не участвует в дальнейшем выборе; при этом количество единиц генеральной совокупности N и отбора. При повторе уменьшается при отборе попавшая в выборку единица возвращается после регистрации в генеральную совокупность и сохраняет таким образом одинаковую возможность вместе с другими единицами быть использованной в последующей процедуре отбора; при этом количество единиц генеральной совокупности N неизменно (способ в социально-экономических исследованиях используется редко). Но, при большом N (N → ∞) формулы для бесповторного отбора можно приблизить к аналогичным для повторного отбора и обычно применяются последние (N = const).

Главные свойства параметров выборочной и генеральной совокупности

В основании статистических выводов проводимого исследования лежит распределение случайной величины, а наблюдаемые значения (х1, х2, … , хn) называют реализациями случайной величины Х (n — объем выборки). Распределение случайной величины в генеральной совокупности имеет идеальный, теоретический характер, а ее выборочный аналог — это эмпирическое распределение. Определенные теоретические распределения аналитически заданы, т.е. их свойства определяют значение функции распределения во всех точках пространства вероятных значений случайной величины. Функцию распределения для выборки определить трудно, а порой невозможно, потому параметры оценивают по эмпирическим данным, а потом их подставляют в аналитическое выражение, которое описывает теоретическое распределение. При этом гипотеза (или предположение) о типе распределения может быть как верным статистически, так и ошибочным. Но как бы там ни было, эмпирическое распределение, которое восстановлено по выборке, только грубо характеризует истинное. Самые важные параметры распределений — это дисперсия и математическое ожидание.

Распределения по своей природе бывают дискретными и непрерывными. Наиболее известное непрерывное распределение — это нормальное распределение. Выборочными аналогами параметров для него являются: эмпирическая дисперсия и среднее значение. В социально-экономических исследованиях среди дискретных чаще всего применяют дихотомическое (альтернативное) распределение. Параметр математического ожидания данного распределения выражает относительную долю (или величину) единиц совокупности, которые имеют изучаемый признак (она обозначается буквой ); доля совокупности, которая не обладает данным признаком, обозначается буквой q (q = 1 — p). Дисперсия альтернативного распределения имеет также эмпирический аналог .

Зависимо от типа распределения и от метода отбора единиц совокупности вычисляются по-разному свойства параметров распределения.

Доля выборки kn — это отношение количества единиц выборочной совокупности к количеству единиц генеральной совокупности:

kn = n/N.

Выборочная доля w — это отношение единиц, которые обладают изучаемым признаком x к объему выборки n:

w = nn/n.

Пример. В партии товара, которая содержит 1000 ед., при 5% выборке доля выборки kn в абсолютной величине имеет 50 ед. (n = N*0,05); когда в данной выборке обнаруживается 2 бракованных изделия, то выборочная доля брака w составит 0,04 (w = 2/50 = 0,04 или 4%).

Так как выборочная совокупность отличается от генеральной, то появляются ошибки выборки.

Ошибки выборки

При каком-либо статистическом наблюдении (выборочном и сплошном) могут встретиться ошибки двух типов: репрезентативности и регистрации. Ошибки регистрации могут иметь систематический и случайный характер. Вероятные ошибки складывают из множества разных неконтролируемых причин, носят непреднамеренный характер и обычно по совокупности друг друга уравновешивают (к примеру, изменения показателей прибора при температурных колебаниях в помещении).

Систематические ошибки являются тенденциозными, так как нарушают правила отбора объектов в выборку (к примеру, отклонения в измерениях при изменении настройки измерительного прибора).

Пример. Для того, чтобы оценить социальное положение населения в городе необходимо обследовать 25% семей. Когда при этом выбор каждой четвертой квартиры основывается на ее номере, то есть опасность отобрать все квартиры лишь одного вида (к примеру, однокомнатные), что снабдит систематическую ошибку и поменяет результаты; выбор же номера квартиры по жребию является более предпочтительным, так как ошибка будет являться случайной.

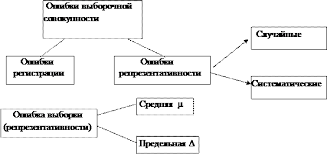
Ошибки репрезентативности являются присущими лишь выборочному наблюдению, их нельзя избежать и они появляются в итоге того, что выборочная совокупность воспроизводит не полностью генеральную. Значения показателей, которые получаются по выборке, отличны от показателей данных величин в генеральной совокупности (или получаемые при сплошном наблюдении).

Ошибка выборочного наблюдения — это разность меж значением параметра в генеральной совокупности и выборочным ее значением. Для среднего значения числового признака она равняется , а для доли (альтернативного признака) — .

Ошибки выборки свойственны лишь выборочным наблюдениям. Чем больше такие ошибки, тем больше эмпирическое распределение от теоретического отличается. Параметры эмпирического распределения являются случайными величинами, поэтому, ошибки выборки являются также случайными величинами, могут принимать для различных выборок различные значения и поэтому обычно вычисляют среднюю ошибку.

Средняя ошибка выборки — это величина, которая выражает квадратическое среднее отклонение выборочной средней от математического ожидания. Данная величина при выполнении принципа случайного отбора прежде всего зависит от объема выборки и от уровня варьирования признака: чем меньше и чем больше вариация признака (соответственно, и значение), тем меньше величина средней ошибки выборки. Соотношение меж дисперсиями выборочной и генеральной совокупностей выражают формулой:

Средняя ошибка выборки указывает вероятные отклонения параметра выборочной совокупности от параметра генеральной.

Но о величине средней ошибки возможно судить только с определенной, вероятностью Р (Р ≤ 1). Ляпунов А.М. доказал, что распределение средних выборочных, a соответственно, и их отклонений от генеральной средней, при довольно большом количестве подчиняется приближенно нормальному закону распределения при условии, что генеральная совокупность имеет конечную среднюю и ограниченную дисперсию.

Следовательно, выражение может быть прочитано так: с вероятностью Р = 0,683 (68,3%) можно полагать, что разница меж генеральной и выборочной средней не больше одной величины средней ошибки m (t = 1), с вероятностью Р = 0,954 (95,4%) — что она не больше величины двух средних ошибок m (t = 2) , с вероятностью Р = 0,997 (99,7%) — не больше трех значений m (t = 3) . Таким образом, вероятность того, что данная разность будет больше трехкратной величины средней ошибки определяет уровень ошибки и составляет не больше 0,3%.

Распространение выборочных результатов на генеральную совокупность

Конечная цель выборочного наблюдения — это характеристика генеральной совокупности. Эмпирические оценки параметров при небольших объемах выборки могут отклоняться существенным образом от их истинных значений. Поэтому появляется необходимость установить границы, в границах которых для выборочных значений параметров лежат истинные значения.

Доверительным интервалом какого-нибудь параметра генеральной совокупности называют случайную область значений данного параметра, которая с вероятностью, которая близка к 1 (надежностью) имеет истинное значение данного параметра.

Граничная ошибка выборки дает возможность определить граничные значения характеристик генеральной совокупности и их доверительные интервалы.

Нижняя граница доверительного интервала получается при помощи вычитания граничной ошибки из выборочного среднего (доли), а верхняя — при помощи ее добавления.

При расчете доверительного интервала для трех доверительных стандартных уровней Р = 95%, Р = 99% и Р = 99,9% значение выбирают по таблице Стьюдента. Приложения зависимо от количества степеней свободы. Когда объем выборки довольно велик, то соответствующие данным вероятностям значения t равняются: 1,96, 2,58 и 3,29. Поэтому граничная ошибка выборки дает возможность определить доверительные интервалы и граничные значения характеристик генеральной совокупности.

Распространение итогов выборочного наблюдения на генеральную совокупность в экономических социальных исследованиях имеет собственные особенности, так как потребует полноты представительности всех ее групп и типов.

Есть два главных способа распространения выборочного наблюдения на генеральную совокупность: способ коэффициентов и прямой пересчет.

Мы коротко рассмотрели выборочное наблюдение: статистическая совокупность выборка и генеральная совокупность, главные методы организации выборки, главные свойства параметров выборочной и генеральной совокупности, ошибки выборки, распространение выборочных результатов на генеральную совокупность. Оставляйте свои комментарии или дополнения к материалу