Добавлено в закладки: 0
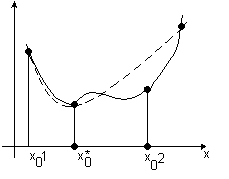 Что такое аппроксимация – это научный метод, который можно использовать в разных областях познания. В дословном переводе он означает «приближение», и под ним подразумевается замена одних объектов, которые изучаются, на другие, схожие с исходными и более простые.
Что такое аппроксимация – это научный метод, который можно использовать в разных областях познания. В дословном переводе он означает «приближение», и под ним подразумевается замена одних объектов, которые изучаются, на другие, схожие с исходными и более простые.
Метод аппроксимации дает возможность проводить исследования разных характеристик объектов, например, их качественных и числовых свойств.
Это достигается тем, что эти свойства сводятся к характеристикам объектов, которые уже известны, или гораздо легче определяются.
Рассмотрим, более детально, что значит аппроксимация. Аппроксима́ция, или приближе́ние являются научным методом, состоящим в замене одних объектов другими, в каком-то смысле близкими к исходным, однако более простыми.
Аппроксимация дает возможность исследовать качественные свойства и количественные характеристики объекта, сводя задачу к изучению более удобных или более простых объектов (к примеру, таких, свойства которых легко вычисляются или свойства которых известны уже). В теории чисел изучают диофантовы приближения, в частности, приближения рациональными иррациональных чисел. В геометрии рассматривают аппроксимации кривых ломаными. Определенные разделы математики целиком посвящены в сущности аппроксимации, к примеру, теория приближения функций, количественные методы анализа.
В переносном смысле употребляют в философии как способ приближения, указание на неокончательный, приблизительный характер. К примеру, в таком смысле термин «аппроксимация» употреблялся активно Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»
Остаточный член
Остаточный член — разница меж аппроксимирующей функцией и заданной функцией. Оценка остаточного члена тем самым является оценкой точности рассматриваемой аппроксимации. Данный термин используется, к примеру, в формуле ряда Тейлора.
Примеры
- Для прибл
 ижённого вычисления интеграла используется формула прямоугольников или формула трапеций, или более сложная квадратурная формула. Фактически при этом происходит приближение подынтегральной функции ступенчатой функцией или вписанной ломаной, интеграл от которой считается мгновенно.
ижённого вычисления интеграла используется формула прямоугольников или формула трапеций, или более сложная квадратурная формула. Фактически при этом происходит приближение подынтегральной функции ступенчатой функцией или вписанной ломаной, интеграл от которой считается мгновенно. - Для вычисления сложных функций зачастую применяется вычисление значения отрезка ряда, который аппроксимирует функцию.
- Для обработки натурных или экспериментальных данных. Тут необходимо рассматривать два случая: 1) аппроксимирующая функция ограничивается диапазоном заданных точек и является только интерполирующей зависимости, не учитывая ошибок; 2) аппроксимирующая функция в роли физического закона выступает и при ее помощи допускают экстраполировать переменные.
Когда функция будет применяться лишь для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:
Гораздо сложней обстоит дело, когда изменения с граничными условиями. Тут уже качество итога зависит от профессионализма исследователя.
Для оптимального выбора параметров уравнений используют обычно способ наименьших квадратов.
Мы надеемся, что дали наиболее полное определение и понятие термина аппроксимация, привели ее примеры


 Аппарат управления
Аппарат управления Аппарат государственный
Аппарат государственный Апостиль
Апостиль Антреприза
Антреприза Антимонопольная политика
Антимонопольная политика Антиномия
Антиномия Антиинфляционная политика
Антиинфляционная политика Аномия
Аномия Аннуитет
Аннуитет Андеррайтер
Андеррайтер Андеррайтинг
Андеррайтинг Аннексия
Аннексия Анклав
Анклав Аналогия
Аналогия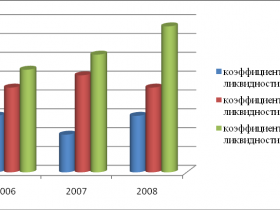 Анализ платежеспособности и ликвидности
Анализ платежеспособности и ликвидности Анализ кластерный
Анализ кластерный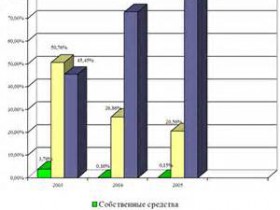 Анализ ликвидности баланса
Анализ ликвидности баланса Аналитик
Аналитик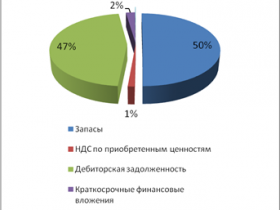 Анализ ликвидности предприятия
Анализ ликвидности предприятия Анализ портфельный
Анализ портфельный Анализ функционально-стоимостной
Анализ функционально-стоимостной